I think that, in order to deal with these things, it might be advantageous to allow the users to define extended objects such as lines and planes. That is, in Ti*k*Z the user can name coordinates and nodes, and, if the `intersections` library is loaded, also paths. Now one can allow users to define lines with e.g. the syntax
```
\path[3d/line through={(A) and (B) named lAB}];
```
which will define `lAB` as the line by creating the necessary internal macros. Likewise, both
```
\path[3d/plane through=(A) and (B) and (C) named pABC];
```
and
```
\path[3d/plane with normal={(1,2,3) through (C) named ptwo}];
```
define planes. As one can see, the input is different in both sample commands, but the internal macros will be the same. One can then involve the plane and line in operations like
```
\path[3d/project={(O) on pABC}] coordinate (E);
```
and
```
\path[3d/project={(C) on lAB}] coordinate (C');
```
which always uses the `project` key, but the code will figure out whether the object it is projecting on is a plane or a line.
Likewise, once you have defined a line through `O` and `D` with
```
\path[3d/line through={(O) and (D) named lOD}];
```
for the intersection of a plane with a line, you can either use
```
\path[3d/intersection of={lOD with pABC}] coordinate (I);
```
or
```
\path[3d/intersection of={pABC with lOD}] coordinate (I);
```
the code works with both inputs. (I personally hate it if I have to remember the order of arguments, so this is an attempt to avoid the need of remembering this here.)
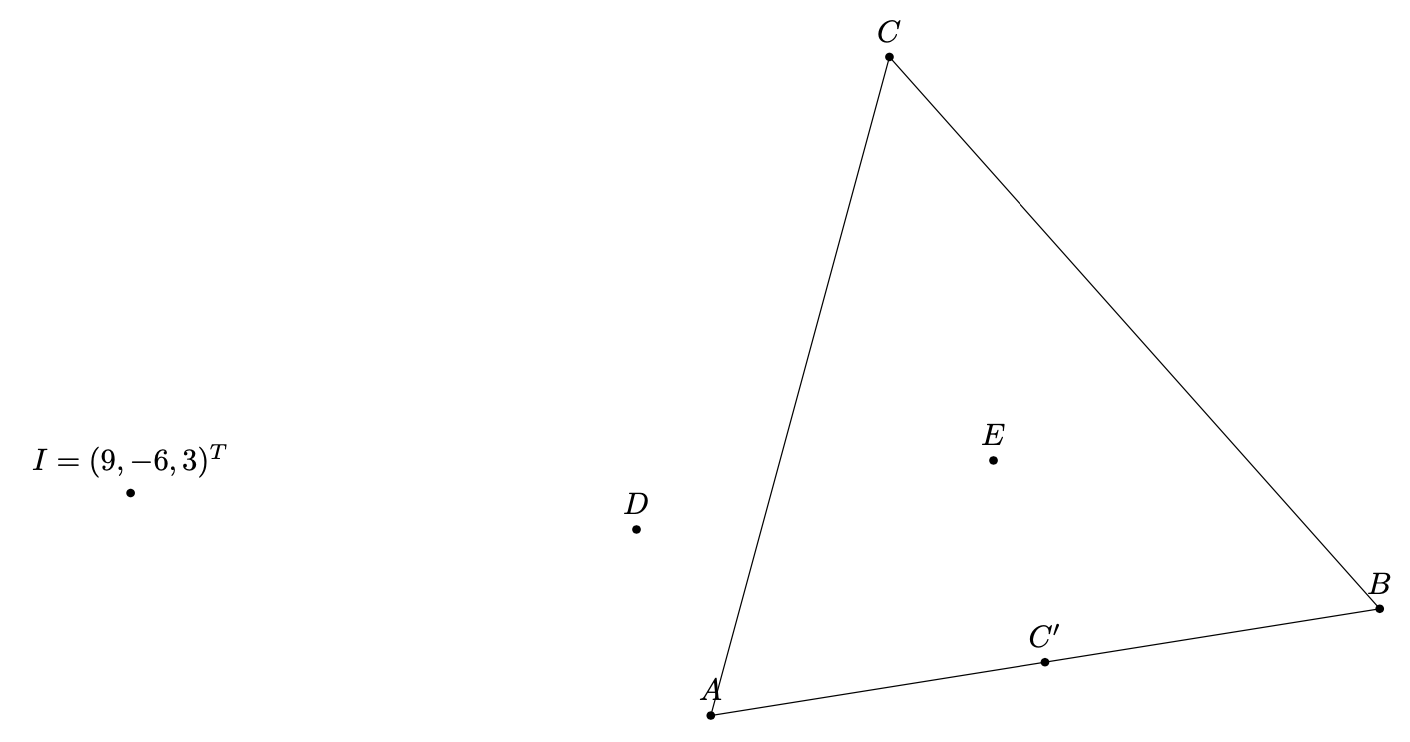
Here is a full example. It relies on to the newest (as of August 21, 2020) version of the [3dtools library](https://github.com/marmotghost/tikz-3dtools).
```
\documentclass[tikz,border=3mm]{standalone}
\usetikzlibrary{3dtools}
\begin{document}
\begin{tikzpicture}[3d/install view={phi=110,psi=0,theta=70},
dot/.style={circle,inner sep=1pt,fill}]
\draw
(0,0,0) coordinate (O)
(6,0,0) coordinate (A) --
(0,6,0) coordinate (B) --
(0,0,6) coordinate (C) -- (A)
(3,-2,1) coordinate (D);
% define plane through three points
\path[3d/plane through=(A) and (B) and (C) named pABC];
% define plane via normal and one point
\path[3d/plane with normal={(1,2,3) through (C) named ptwo}];
% define line through two points
\path[3d/line through={(A) and (B) named lAB}];
\path[3d/line through={(O) and (D) named lOD}];
% project point on plane
\path[3d/project={(O) on pABC}] coordinate (E);
% project point on line
\path[3d/project={(C) on lAB}] coordinate (C');
% intersection of line O--D with plane through A, B and C
\path[3d/intersection of={lOD with pABC}] coordinate (I);
% you can swap the order of arguments, it still works:
%\path[3d/intersection of={pABC with lOD}] coordinate (I);
% visualize the points
\path foreach \X in {A,...,E,C'}
{(\X) coordinate[dot,label=above:{$\X$}]};
\path (I) coordinate[dot,label=above:{$I=\pgfmathparse{TD("(I)")}%
(\pgfmathprintvector\pgfmathresult)^T
$}];
\end{tikzpicture}
\end{document}
```
The computations going into these codes are elementary, but since I am very good at introducing typos I add them so that one can find bugs more easily.
```
\documentclass[fleqn,10pt]{article}
\usepackage[margin=1in]{geometry}
\usepackage{amsmath}
\usepackage{hyperref}
\begin{document}
This is an analytic discussion of some of the computations in 3d that got
implemented in the \href{https://github.com/marmotghost/tikz-3dtools}{3dtools}
library. This discussion concerns
\begin{itemize}
\item the projection of a point on a line,
\item the projection of a point on a plane, and
\item the intersection of a line and a plane.
\end{itemize}
In what follows, we will denote the points that define the line $\vec A$ and
$\vec B$, the normal of the plane $\vec n$ and $\vec C$ a point that is
contained in the plane.
\subsection*{Projection of a point on a line}
The projection of a point $\vec P$ is a point on the line, i.e.
\[\vec P'=\vec A+\alpha\,\left(\vec B-\vec A\right)\;.\]
The projection is defined by the requirement that $\vec P-\vec P'\perp\vec
A-\vec B$,
\begin{align*}
0&\overset{!}{=}
\left(\vec P-\vec P'\right)\cdot\left(\vec A-\vec B\right)\\
&=\vec P\cdot\left(\vec A-\vec B\right)
-\vec A\cdot\left(\vec A-\vec B\right)
-\alpha\,\left(\vec B-\vec A\right)\cdot\left(\vec B-\vec A\right)\;,
\end{align*}
i.e.\
\[
\alpha=\frac{\left(\vec P-\vec A\right)\cdot\left(\vec B-\vec A\right)}{%
\left(\vec B-\vec A\right)\cdot\left(\vec B-\vec A\right)}\;.
\]
\subsection*{Projection of a point on a plane}
The projection of a point $\vec P$ on a plane is the intersection of the line
through $\vec P$ along the normal $\vec n$ and the plane. That is, we need to
solve
\[
\vec n\cdot\left(\vec P+\alpha\,\vec n\right)
=\vec n\cdot \vec C\;,
\]
i.e.\
\[
\alpha=\frac{\vec n\cdot\left(\vec C-\vec P\right)}{\vec n\cdot\vec n}
\;.
\]
\subsection*{Intersection of a line and a plane}
The condition for a point $\vec P$ sitting on the line $\vec A-\vec B$ is
\[ \vec P=\vec A+\alpha\,\left(\vec B-\vec A\right)\;,\]
and the condition for $\vec P$ being on the plane is
\[
\vec n\cdot \vec P=\vec n\cdot \vec C\;,
\]
so
\[
\alpha=\frac{\vec n\cdot\left(\vec C-\vec A\right)}{%
\vec n\cdot\left(\vec B-\vec A\right)}\;.
\]
\end{document}
```
