How can I draw a sphere inscribed a cone? - TeX

TopAnswers TeX

Top Answer

user 3.14159

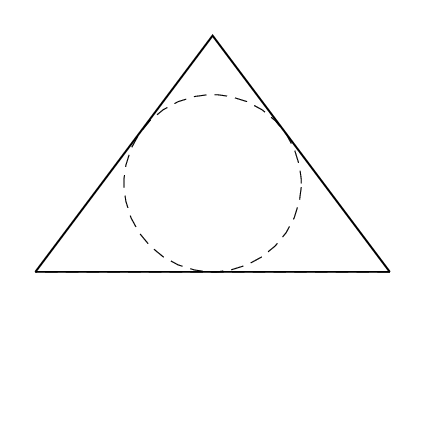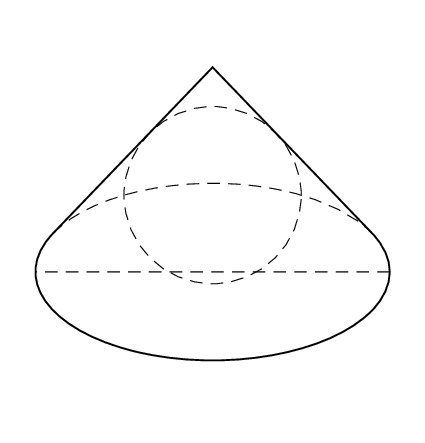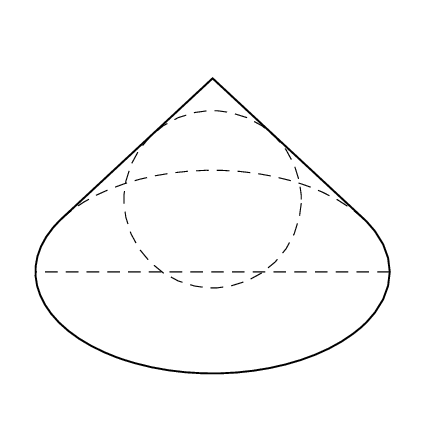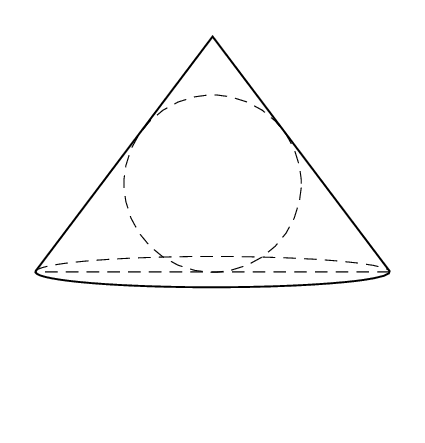
You did already the most complicated part, the computation of the radius. The rest is comparatively simple, also because I had a code for drawing cones on my hard drive anyway.

```
\documentclass[tikz,border=3mm]{standalone}
\usepackage{tikz-3dplot}
\usetikzlibrary{3dtools}
\tikzset{pics/3d/cone/.style={code={
	\tikzset{3d/cone/.cd,#1}
	\def\pv##1{\pgfkeysvalueof{/tikz/3d/cone/##1}}%
	\pgfmathsetmacro{\sdtip}{screendepth(0,0,\pv{h})}
	\pgfmathsetmacro{\aspectangle}{atan2(\sdtip,sqrt(\pv{h}*\pv{h}-\sdtip*\sdtip))}
	\path (0,0,\pv{h}) coordinate (-tip);
    \begin{scope}[x={(0,0,tan(\aspectangle))},y={($(0,0,0)!1cm!90:(0,0,\pv{h})$)}]
	 \pgfmathtruncatemacro{\itest}{abs(tan(\aspectangle)*\pv{r}/\pv{h})<1}
	 \ifnum\itest=1
	  \pgfmathsetmacro{\alphacrit}{acos(tan(\aspectangle)*\pv{r}/\pv{h})}
	  \ifdim\sdtip pt>0pt
	   \path[/tikz/3d/cone/hidden] (\alphacrit:\pv{r}) arc[start angle=\alphacrit,end
	   angle=-\alphacrit,radius=\pv{r}];
	   \path[/tikz/3d/cone/visible] (\alphacrit:\pv{r}) 
	   arc[start angle=\alphacrit,end  angle=360-\alphacrit,radius=\pv{r}]
	   -- (-tip) -- cycle;
	  \else
	   \path[/tikz/3d/cone/visible] circle[radius=\pv{r}];
	   \path[/tikz/3d/cone/visible] (\alphacrit:\pv{r}) 
	   -- (-tip) -- (360-\alphacrit:\pv{r});
	  \fi
	 \else
	  \path[/tikz/3d/cone/visible] circle[radius=\pv{r}];	 
	 \fi
    \end{scope}
	}},
	3d/cone/.cd,r/.initial=1,h/.initial=1,
	hidden/.style={draw,very thin,densely dashed},
	visible/.style=draw}
\begin{document}
\begin{tikzpicture}[,declare function={
 	r=1.5;h=2;rs=(r*sqrt(h^2+r^2)-r^2)/h);
 	}]
 \tdplotsetmaincoords{70}{110}
 \begin{scope}[tdplot_main_coords]
  \pic{3d/cone={r=r,h=h}};
  \path (0,0,rs) coordinate (cs);
 \end{scope}
 \draw[3d/cone/hidden] (cs) circle[radius=rs];
\end{tikzpicture}
\end{document}
```
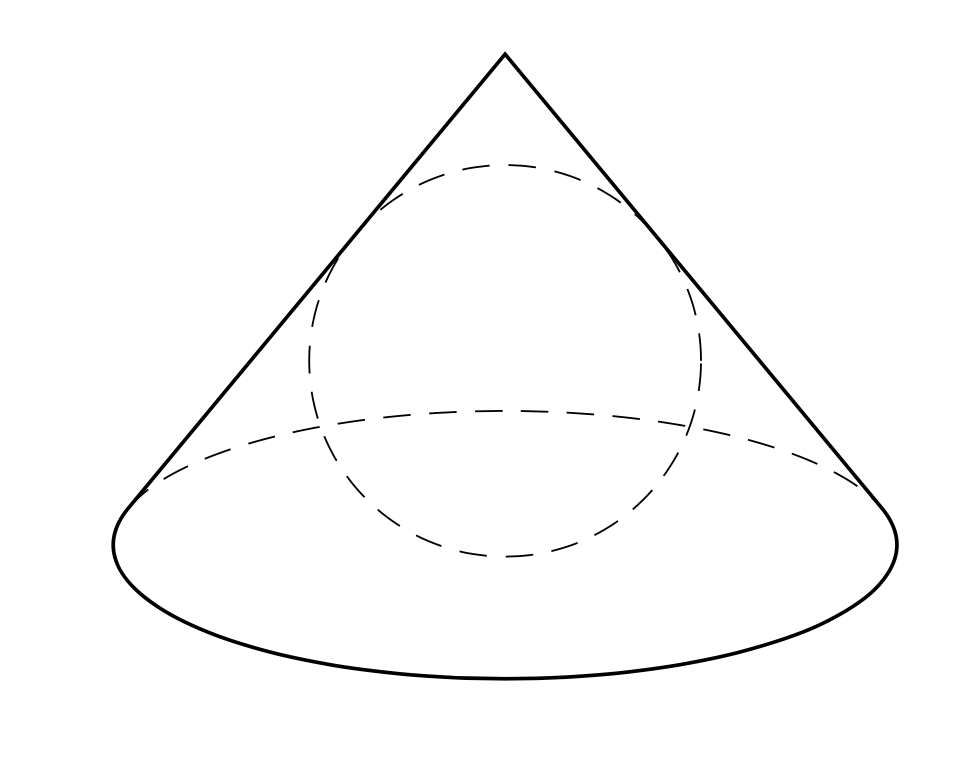
![Screen Shot 2020-08-16 at 9.07.15 AM.png](/image?hash=0e076d4cb1514a9fc69ea92e31e345b58219648ccb9c31a85133d60f32dbac5b)

Of course, the sphere does not change its radius when altering the view angles, and the projection of a sphere on the screen is a circle of the radius of the sphere. So this circle won't change when we animate the view angles. 
```
\documentclass[tikz,border=3mm]{standalone}
\usepackage{tikz-3dplot}
\usetikzlibrary{3dtools}
\tikzset{pics/3d/cone/.style={code={
	\tikzset{3d/cone/.cd,#1}
	\def\pv##1{\pgfkeysvalueof{/tikz/3d/cone/##1}}%
	\pgfmathsetmacro{\sdtip}{screendepth(0,0,\pv{h})}
	\pgfmathsetmacro{\aspectangle}{atan2(\sdtip,sqrt(\pv{h}*\pv{h}-\sdtip*\sdtip))}
	\path (0,0,\pv{h}) coordinate (-tip);
    \begin{scope}[x={(0,0,tan(\aspectangle))},y={($(0,0,0)!1cm!90:(0,0,\pv{h})$)}]
	 \pgfmathtruncatemacro{\itest}{abs(tan(\aspectangle)*\pv{r}/\pv{h})<1}
	 \ifnum\itest=1
	  \pgfmathsetmacro{\alphacrit}{acos(tan(\aspectangle)*\pv{r}/\pv{h})}
	  \ifdim\sdtip pt>0pt
	   \path[/tikz/3d/cone/hidden] (\alphacrit:\pv{r}) arc[start angle=\alphacrit,end
	   angle=-\alphacrit,radius=\pv{r}];
	   \path[/tikz/3d/cone/visible] (\alphacrit:\pv{r}) 
	   arc[start angle=\alphacrit,end  angle=360-\alphacrit,radius=\pv{r}]
	   -- (-tip) -- cycle;
	  \else
	   \path[/tikz/3d/cone/visible] circle[radius=\pv{r}];
	   \path[/tikz/3d/cone/visible] (\alphacrit:\pv{r}) 
	   -- (-tip) -- (360-\alphacrit:\pv{r});
	  \fi
	 \else
	  \path[/tikz/3d/cone/visible] circle[radius=\pv{r}];	 
	 \fi
    \end{scope}
	}},
	3d/cone/.cd,r/.initial=1,h/.initial=1,
	hidden/.style={draw,very thin,densely dashed},
	visible/.style=draw}
\begin{document}
\foreach \Angle in {90,85,...,40,45,50,...,85}
{\begin{tikzpicture}[,declare function={
 	r=1.5;h=2;rs=(r*sqrt(h^2+r^2)-r^2)/h);
 	}]
 \path[use as bounding box] (-r,{r*cos(140)}) rectangle (r,h);
 \tdplotsetmaincoords{\Angle}{0}
 \begin{scope}[tdplot_main_coords]
  \pic{3d/cone={r=r,h=h}};
  \draw[3d/cone/hidden,canvas is xy plane at z=0] (00:r) -- (180:r);
  \path (0,0,rs) coordinate (cs);
 \end{scope}
 \draw[3d/cone/hidden] (cs) circle[radius=rs];
\end{tikzpicture}}
\end{document}
```
![ani.gif](/image?hash=72d88181867697d705180ee6f3ca64850a62d074cb0a0ba80db4fbdb02dc0e45)

I think that they construct the boundary of the sphere by demanding that the corresponding circle touches the boundary of the cones, If you know the radius, this is a valid method (and can be shortened quite a bit). However, I do not think that the equator circle is correct, maybe it is just not meant to be an equator.

@marmot, re: [your answer](#a1471), [This paper](https://www.researchgate.net/publication/315620080_Latex_as_an_Ideal_Tool_for_Integration_of_ICT_and_Mathematics_in_Science_Teaching#pf5) show some incorrect figures and use Tikz Euclide to correct them

I added a `shaded cone` pic to `3dtools`. ``` \documentclass[tikz,border=3mm]{standalone} \usetikzlibrary{calc,3dtools} \begin{document} \foreach \Angle in {5,15,...,355} {\begin{tikzpicture}[same bounding box=A] \begin{scope}[3d/install view={phi=110,psi=0,theta=\Angle}] \path pic{3d/shaded cone={r=2,h=3}}; \end{scope} \end{tikzpicture}} \end{document} ``` ![ani.gif](/image?hash=d8a9ad7a05dea73206ae1e17dfd37b24569242ce9d077706ec604508c0774e29)

The problem is not so much the computation of the visible stretches and so on, which is under control, I think. The problem is to make a cone look like a cone when you look at it from the top. The good news is that there are enough explanations in [Symbol 1's answer](https://tex.stackexchange.com/a/333409) to get something reasonable (and the pgfmanual is not too helpful in this regard, it was better before guesswork was presented as facts). Anyway, thanks to this post and [Mark Wibrow's post](https://tex.stackexchange.com/a/185920) I now can produce things like ![Screen Shot 2021-03-24 at 8.26.15 PM.png](/image?hash=20cead55e0c4ea8eddb40df73391aed42d7f401e6dffc828bd9b00cf402335f9)

Sadly it does not work for all view angles. ``` \documentclass[tikz,border=3mm]{standalone} \usetikzlibrary{calc,decorations.pathreplacing,3dtools}%https://github.com/marmotghost/tikz-3dtools \begin{document} \pgfdeclarelayer{background} \pgfdeclarelayer{foreground} \pgfsetlayers{background,main,foreground} \foreach \Angle in {5,15,...,355} {\begin{tikzpicture}[declare function={R=2;},line cap=round,line join=round, sphere/.style={ball color=blue,3d/screen coords,fill opacity=0.8, insert path={(0,0) circle[radius=R]}}] \begin{scope}[3d/install view={phi=110,psi=0,theta=\Angle}] \path (0,0,0) coordinate (O) (0,0,1) coordinate (P); \draw[stored path/reset coordinate index, 3d/hidden/.style={store path=bg}, 3d/visible/.append style={on layer=foreground}] pic{3d/circle on sphere={R=2,P={(P)}}}; \pgfmathtruncatemacro{\Nhid}{tikztdindexoflastcoordinate} \ifnum\Nhid>0 \path[stored path/first coordinate of=bg] coordinate (bg0) [stored path/last coordinate of=bg] coordinate (bg1); \fi \draw[stored path/reset coordinate index, 3d/hidden/.append style={on layer=background}, 3d/visible/.style={store path=fg}] pic{3d/circle on sphere={R=2,P={(P)}}}; \pgfmathtruncatemacro{\Nvis}{tikztdindexoflastcoordinate} \ifnum\Nvis>0 \path[stored path/first coordinate of=fg] coordinate (fg0) [stored path/last coordinate of=fg] coordinate (fg1); \fi \pgfmathtruncatemacro{\itest}{(\Nhid>0?1:0)+(\Nvis>0?2:0)} \begin{scope}[3d/screen coords] \ifcase\itest % no path \or % only hidden \begin{scope}[on layer=background] \clip[stored path/restore path=bg]; \path[sphere,ball color=gray]; \end{scope} \or % only visible \begin{scope}[on layer=foreground] \clip[stored path/restore path=fg]; \path[sphere]; \end{scope} \or \begin{scope}[on layer=background] \clip let \p1=(bg0),\p2=(bg1),\n1={Mod(atan2(\y1,\x1),360)}, \n2={Mod(atan2(\y2,\x2),360)} in (bg0) [stored path/append path=bg] -- (bg1) arc[start angle=\n2,end angle=\n1,radius=R] -- cycle; \path[sphere,ball color=gray]; \end{scope} \begin{scope}[on layer=foreground] \clip let \p1=(fg0),\p2=(fg1),\n1={Mod(atan2(\y1,\x1),360)}, \n2={Mod(atan2(\y2,\x2),360)} in (fg0) [stored path/append path=fg] -- (fg1) arc[start angle=\n2,end angle=\n1,radius=R] -- cycle; \path[sphere]; \end{scope} \fi \end{scope} \pgfmathsetmacro{\myh}{tddistance("(O)","(P)")} \pgfmathsetmacro{\myr}{sqrt(R*R-\myh*\myh)} \path (1,0,0) coordinate (ex) (0,1,0) coordinate (ey) (0,0,-1) coordinate (ez'); \begin{scope}[x={(ex)},y={(ey)},z={(ez')}] \path[shift={(P)}, 3d/cone/outer/.style={left color=gray!40,right color=gray!80,middle color=gray!10}, 3d/cone/inner/.style={left color=gray!60,right color=gray!80!black,middle color=gray!40} ] pic{3d/cone={r=\myr,h=\myh}}; \end{scope} \draw[3d/visible,3d/screen coords] circle[radius=R]; \end{scope} \end{tikzpicture}} \end{document} ```

``` \documentclass[tikz,border=3mm]{standalone} \usetikzlibrary{calc,decorations.pathreplacing,3dtools}%https://github.com/marmotghost/tikz-3dtools \begin{document} \pgfdeclarelayer{background} \pgfdeclarelayer{foreground} \pgfsetlayers{background,main,foreground} \foreach \Angle in {5,15,...,355} {\begin{tikzpicture}[declare function={R=2;},line cap=round,line join=round, sphere/.style={ball color=blue,3d/screen coords,fill opacity=0.8, insert path={(0,0) circle[radius=R]}}] \begin{scope}[3d/install view={phi=110,psi=0,theta=\Angle}] \path (0,0,1) coordinate (P); \draw[stored path/reset coordinate index, 3d/hidden/.style={store path=bg}, 3d/visible/.append style={on layer=foreground}] pic{3d/circle on sphere={R=2,P={(P)}}}; \pgfmathtruncatemacro{\Nhid}{tikztdindexoflastcoordinate} \ifnum\Nhid>0 \path[stored path/first coordinate of=bg] coordinate (bg0) [stored path/last coordinate of=bg] coordinate (bg1); \fi \draw[stored path/reset coordinate index, 3d/hidden/.append style={on layer=background}, 3d/visible/.style={store path=fg}] pic{3d/circle on sphere={R=2,P={(P)}}}; \pgfmathtruncatemacro{\Nvis}{tikztdindexoflastcoordinate} \ifnum\Nvis>0 \path[stored path/first coordinate of=fg] coordinate (fg0) [stored path/last coordinate of=fg] coordinate (fg1); \fi \pgfmathtruncatemacro{\itest}{(\Nhid>0?1:0)+(\Nvis>0?2:0)} \begin{scope}[3d/screen coords] \ifcase\itest % no path \or % only hidden \begin{scope}[on layer=background] \clip[stored path/restore path=bg]; \path[sphere]; \end{scope} \or % only visible \clip[stored path/restore path=fg]; \path[sphere]; \or \begin{scope}[on layer=background] \clip let \p1=(bg0),\p2=(bg1),\n1={Mod(atan2(\y1,\x1),360)}, \n2={Mod(atan2(\y2,\x2),360)} in (bg0) [stored path/append path=bg] -- (bg1) arc[start angle=\n2,end angle=\n1,radius=R] -- cycle; \path[sphere]; \end{scope} \begin{scope} \clip let \p1=(fg0),\p2=(fg1),\n1={Mod(atan2(\y1,\x1),360)}, \n2={Mod(atan2(\y2,\x2),360)} in (fg0) [stored path/append path=fg] -- (fg1) arc[start angle=\n2,end angle=\n1,radius=R] -- cycle; \path[sphere]; \end{scope} \fi \end{scope} \draw[3d/visible,3d/screen coords] circle[radius=R]; \end{scope} \end{tikzpicture}} \end{document} ```

``` \documentclass[tikz,border=3mm]{standalone} \usetikzlibrary{calc,3dtools}%https://github.com/marmotghost/tikz-3dtools \begin{document} \begin{tikzpicture}[declare function={R=2;alpha=30;beta=50;}] \begin{scope}[3d/install view={phi=110,psi=0,theta=70}] %\pgfmathsetmacro\sdA{screendepth({R*cos(alpha)},{R*sin(alpha)},0)} %\pgfmathsetmacro\sdB{screendepth({R*cos(beta)},{R*sin(beta)},0)} % critical angles \pgfmathsetmacro{\tcritA}{atan2(nscreenx*cos(alpha)+nscreeny*sin(alpha),-1*nscreenz)-180} \pgfmathsetmacro{\tcritB}{atan2(nscreenx*cos(beta)+nscreeny*sin(beta),-1*nscreenz)-180} \path ({R*cos(alpha)*cos(\tcritA)},{R*sin(alpha)*cos(\tcritA)},{R*sin(\tcritA)}) coordinate (pA) ({R*cos(beta)*cos(\tcritB)},{R*sin(beta)*cos(\tcritB)},{R*sin(\tcritA)}) coordinate (pB); \path[fill=gray!20,smooth] plot[variable=\t,domain=90:-90] ({R*cos(alpha)*cos(\t)},{R*sin(alpha)*cos(\t)},{R*sin(\t)}); \draw[3d/hidden,smooth] plot[variable=\t,domain=\tcritA:-90] ({R*cos(alpha)*cos(\t)},{R*sin(alpha)*cos(\t)},{R*sin(\t)}) -- (0,0,R); \draw[3d/visible,3d/screen coords] circle[radius=R]; \draw[3d/visible,fill=gray,smooth] plot[variable=\t,domain=\tcritA:90] ({R*cos(alpha)*cos(\t)},{R*sin(alpha)*cos(\t)},{R*sin(\t)}) -- plot[variable=\t,domain=90:\tcritB] ({R*cos(beta)*cos(\t)},{R*sin(beta)*cos(\t)},{R*sin(\t)}) [3d/screen coords] let \p1=(pA),\p2=(pB), \n1={atan2(\y1,\x1)},\n2={atan2(\y2,\x2)} in arc[start angle=\n2,end angle=\n1,radius=R]; \end{scope} \end{tikzpicture} \end{document} ``` ![Screen Shot 2021-03-22 at 6.06.32 AM.png](/image?hash=9e603c90c3539759655883a7785bc512e730cc0810e805fc49046102ce1208ce)

Maybe like this? ``` \documentclass[border=2mm]{standalone} \usepackage{tikz} \begin{document} \begin{tikzpicture}[declare function={r=1;}, c/.style={circle,draw,inner sep=0pt,minimum size=r*2cm}] \draw (-r,0)node[c]{}--(r,0)node[c]{}--(0,{sqrt(3)*r})node[c]{}--cycle (0,{2*r +sqrt(3)*r} )--({-r-r*sqrt(3)},-r)--({r +r*sqrt(3)} ,-r)--cycle; \end{tikzpicture} \end{document} ```

I rarely draw with 2D.I am trying to draw this figure. I tried. ``` \documentclass[border=2mm]{standalone} \usepackage{tikz} \begin{document} \begin{tikzpicture}[line cap=round,line join=round,declare function={r=2; a=2*r*sqrt(3) + 2*r;}] \draw (0,0) circle[radius=r]; \draw (r,{r*sqrt(3)}) circle[radius=r]; \draw (2*r,0) circle[radius=r]; \draw (0,0)--(2*r,0)--(r,{sqrt(3)*r})--cycle; \draw (r,{2*r +sqrt(3)*r} )--(-{r*sqrt(3)},-r)--({2*r +r*sqrt(3)} ,-r)--cycle; \end{tikzpicture} \end{document} ``` How can I reduce this code?

You had the circle outside of the scope that installs the view. If you move it inside, it works. ``` \documentclass[tikz,border=3mm]{standalone} \usepackage{tikz-3dplot} \usetikzlibrary{3dtools} \tikzset{pics/3d/cone/.style={code={ \tikzset{3d/cone/.cd,#1} \def\pv##1{\pgfkeysvalueof{/tikz/3d/cone/##1}}% \pgfmathsetmacro{\sdtip}{screendepth(0,0,\pv{h})} \pgfmathsetmacro{\aspectangle}{atan2(\sdtip,sqrt(\pv{h}*\pv{h}-\sdtip*\sdtip))} \path (0,0,\pv{h}) coordinate (-tip); \begin{scope}[x={(0,0,tan(\aspectangle))},y={($(0,0,0)!1cm!90:(0,0,\pv{h})$)}] \pgfmathtruncatemacro{\itest}{abs(tan(\aspectangle)*\pv{r}/\pv{h})<1} \ifnum\itest=1 \pgfmathsetmacro{\alphacrit}{acos(tan(\aspectangle)*\pv{r}/\pv{h})} \ifdim\sdtip pt>0pt \path[/tikz/3d/cone/hidden] (\alphacrit:\pv{r}) arc[start angle=\alphacrit,end angle=-\alphacrit,radius=\pv{r}]; \path[/tikz/3d/cone/visible] (\alphacrit:\pv{r}) arc[start angle=\alphacrit,end angle=360-\alphacrit,radius=\pv{r}] -- (-tip) -- cycle; \else \path[/tikz/3d/cone/visible] circle[radius=\pv{r}]; \path[/tikz/3d/cone/visible] (\alphacrit:\pv{r}) -- (-tip) -- (360-\alphacrit:\pv{r}); \fi \else \path[/tikz/3d/cone/visible] circle[radius=\pv{r}]; \fi \end{scope} }}, 3d/cone/.cd,r/.initial=1,h/.initial=1, hidden/.style={draw,very thin,densely dashed}, visible/.style=draw} \begin{document} \begin{tikzpicture}[,declare function={ r=6;h=5;rs=(r*sqrt(h^2+r^2)-r^2)/h); a = -30;b=a + acos(-1/2);}] \tdplotsetmaincoords{70}{110} \begin{scope}[tdplot_main_coords] \pic{3d/cone={r=r,h=h}}; \path (0,0,rs) coordinate (I) (0,0,0) coordinate (O) (0,0,h) coordinate (S) ({r*cos(a)}, {r*sin(a)},0) coordinate (A) ({r*cos(b)}, {r*sin(b)},0) coordinate (B) [3d coordinate={(M)=0.5*(A)+0.5*(B)}]; \path[3d/line through={(S) and (M) named lSM}]; \path[3d/project={(O) on lSM}] coordinate (H); \path pic[red,dashed]{3d incircle={A={(A)},B={(B)},C={(S)},center name=G}}; \end{scope} %\begin{scope}[tdplot_screen_coords] %\fill[ball color=green, opacity=0.8] (I) circle (rs); %\end{scope} \foreach \p in {I,A,B,M,S,O,H} \draw[fill=black] (\p) circle (1.2 pt); \foreach \p/\g in {I/180,A/-90,B/-90,M/-90,S/90,O/-90,H/0} \path (\p)+(\g:3mm) node{$\p$}; \draw (S) -- (A) (S) -- (B); \draw[dashed] (S) -- (O) (A) -- (O) -- (B) -- cycle (S) -- (M) (O) -- (M) (O) --(H); \end{tikzpicture} \end{document} ```

@marmot, re: [your answer](#a1471), I cannot ger correct result when I draw ` \path pic[red,dashed]{3d incircle={A={(A)},B={(B)},C={(S)},center name=G}};` Full code ```\documentclass[tikz,border=3mm]{standalone} \usepackage{tikz-3dplot} \usetikzlibrary{3dtools} \tikzset{pics/3d/cone/.style={code={ \tikzset{3d/cone/.cd,#1} \def\pv##1{\pgfkeysvalueof{/tikz/3d/cone/##1}}% \pgfmathsetmacro{\sdtip}{screendepth(0,0,\pv{h})} \pgfmathsetmacro{\aspectangle}{atan2(\sdtip,sqrt(\pv{h}*\pv{h}-\sdtip*\sdtip))} \path (0,0,\pv{h}) coordinate (-tip); \begin{scope}[x={(0,0,tan(\aspectangle))},y={($(0,0,0)!1cm!90:(0,0,\pv{h})$)}] \pgfmathtruncatemacro{\itest}{abs(tan(\aspectangle)*\pv{r}/\pv{h})<1} \ifnum\itest=1 \pgfmathsetmacro{\alphacrit}{acos(tan(\aspectangle)*\pv{r}/\pv{h})} \ifdim\sdtip pt>0pt \path[/tikz/3d/cone/hidden] (\alphacrit:\pv{r}) arc[start angle=\alphacrit,end angle=-\alphacrit,radius=\pv{r}]; \path[/tikz/3d/cone/visible] (\alphacrit:\pv{r}) arc[start angle=\alphacrit,end angle=360-\alphacrit,radius=\pv{r}] -- (-tip) -- cycle; \else \path[/tikz/3d/cone/visible] circle[radius=\pv{r}]; \path[/tikz/3d/cone/visible] (\alphacrit:\pv{r}) -- (-tip) -- (360-\alphacrit:\pv{r}); \fi \else \path[/tikz/3d/cone/visible] circle[radius=\pv{r}]; \fi \end{scope} }}, 3d/cone/.cd,r/.initial=1,h/.initial=1, hidden/.style={draw,very thin,densely dashed}, visible/.style=draw} \begin{document} \begin{tikzpicture}[,declare function={ r=6;h=5;rs=(r*sqrt(h^2+r^2)-r^2)/h); a = -30;b=a + acos(-1/2);}] \tdplotsetmaincoords{70}{110} \begin{scope}[tdplot_main_coords] \pic{3d/cone={r=r,h=h}}; \path (0,0,rs) coordinate (I) (0,0,0) coordinate (O) (0,0,h) coordinate (S) ({r*cos(a)}, {r*sin(a)},0) coordinate (A) ({r*cos(b)}, {r*sin(b)},0) coordinate (B) [3d coordinate={(M)=0.5*(A)+0.5*(B)}]; \path[3d/line through={(S) and (M) named lSM}]; \path[3d/project={(O) on lSM}] coordinate (H); \end{scope} \path pic[red,dashed]{3d incircle={A={(A)},B={(B)},C={(S)},center name=G}}; %\begin{scope}[tdplot_screen_coords] %\fill[ball color=green, opacity=0.8] (I) circle (rs); %\end{scope} \foreach \p in {I,A,B,M,S,O,H} \draw[fill=black] (\p) circle (1.2 pt); \foreach \p/\g in {I/180,A/-90,B/-90,M/-90,S/90,O/-90,H/0} \path (\p)+(\g:3mm) node{$\p$}; \draw (S) -- (A) (S) -- (B); \draw[dashed] (S) -- (O) (A) -- (O) -- (B) -- cycle (S) -- (M) (O) -- (M) (O) --(H); \end{tikzpicture} \end{document} ```. How can get correct result?

1 Answer