How to draw four spheres in this problem with another way? - TeX

TopAnswers TeX

Meta

Databases

TeX

Code Golf

APL

C++

.net

db<>fiddle

Java

*nix

PHP

PowerShell

Python

Rust

टेक्-मराठी

Typst

Web Client Dev

Web Server Dev

How to draw four spheres in this problem with another way?

add tag

Anonymous 1123

I want to draw picture of this problem 
https://artofproblemsolving.com/wiki/index.php/2004_AMC_12A_Problems/Problem_22
I tried

```
\documentclass[12pt,border=3mm]{standalone}
\usepackage{tikz}
\usepackage{tikz-3dplot}
\usetikzlibrary{calc,backgrounds}
\begin{document}
 \tdplotsetmaincoords{60}{120}
\begin{tikzpicture}
[scale=2,tdplot_main_coords]
\path
coordinate (A) at (0,0,0)
coordinate (B) at  (0,2,0)
coordinate (C) at  (1,{sqrt(3)},0)
coordinate (M) at ($(B)!0.5!(C)$)
coordinate (M) at ($(B)!0.5!(C)$)
coordinate (G) at ($(A)!2/3!(M)$)
coordinate (S) at  (1/3,{(2+sqrt(3))/3},{sqrt(69)/3})
;
\foreach \v/\position in {A/left,B/below,C/below,S/above,G/left} {\draw[draw =black, fill=black] (\v) circle (1.2pt) node [\position=0.2mm] {$\v$};}
\begin{scope}[tdplot_screen_coords, on background layer]
\pgfmathsetmacro{\R}{1}%
\fill[ball color=red!80, opacity=1.0] (A) circle (\R);
\fill[ball color=orange!90, opacity=1.0] (B) circle (\R);
\fill[ball color=blue!70, opacity=1.0] (C) circle (\R);
\fill[ball color=cyan!90, opacity=1.0] (S) circle (2*\R);
\end{scope}
\draw[thick, dashed] (S) -- (A) (S)--(B) (S)--(C) (A)--(B) (A)--(C) (B)--(C) (A)--(G) (B)--(G) (C)--(G) (S)--(G);
\end{tikzpicture}
\end{document}
```
![ScreenHunter 758.png](/image?hash=69136cec76992b83076b517ecac5ca83d836611c1fa758560da9b8b535896d46)

How to draw  four spheres in this problem with another way?

Top Answer

user 3.14159

You have already solved most of the problems, the only step that appears to remain is to put the spheres in 3d order. This can be done by computing the screen depths of some appropriate coordinates and draw the spheres on the respective layers. To simplify this task I have used slightly different coordinates, which I also store in functions like `Ax` and so on.

```
\documentclass[tikz,border=3mm]{standalone}
\usepackage{tikz-3dplot}
\usetikzlibrary{backgrounds,fpu}% calc gets loaded by tikz-3dplot
\makeatletter
% projection of a 3d coordinate on the normal of the screen
\pgfmathdeclarefunction{screendepth}{3}{%
\begingroup%
\pgfkeys{/pgf/fpu,/pgf/fpu/output format=fixed}%
\pgfmathparse{%
((\the\pgf@yx/1cm)*(\the\pgf@zy/1cm)-(\the\pgf@yy/1cm)*(\the\pgf@zx/1cm))*(#1)+
((\the\pgf@zx/1cm)*(\the\pgf@xy/1cm)-(\the\pgf@xx/1cm)*(\the\pgf@zy/1cm))*(#2)+
((\the\pgf@xx/1cm)*(\the\pgf@yy/1cm)-(\the\pgf@yx/1cm)*(\the\pgf@xy/1cm))*(#3)}%
\pgfmathsmuggle\pgfmathresult\endgroup%
}%
% position of a real in a list of reals
\pgfmathdeclarefunction*{pos}{2}{%
\begingroup%
\c@pgf@counta=1%
\pgfutil@for\my@item:={#2}\do{%
\ifdim\my@item pt<#1pt%
\advance\c@pgf@counta by1%
\fi}%
\edef\pgfmathresult{\the\c@pgf@counta}%
\pgfmathsmuggle\pgfmathresult\endgroup%
}
\makeatother
\newcounter{tdorder}
\begin{document}
\foreach \X in {1,...,4}
{\pgfdeclarelayer{layer\X}}
\pgfsetlayers{layer1,layer2,layer3,layer4,main}
\foreach \Angle in {5,15,...,355}
{\tdplotsetmaincoords{70}{\Angle}
 \begin{tikzpicture}[scale=2,tdplot_main_coords,
	 dot/.style={circle,fill,inner sep=0pt,minimum size=2.4pt},
	 declare function={R=1;a=R/sin(60);
		 Ax=a*cos(-30);Ay=a*sin(-30);
		 Bx=0;By=R;
		 Cx=a*cos(210);Cy=a*sin(210);
		 Sz=R*sqrt(69)/3;
		 alpha=atan2(Sz,R);
		 xi=sin(alpha);}]
  \path (Ax,Ay,0) coordinate (A)
	(Bx,By,0) coordinate (B) 
	(Cx,Cy,0) coordinate (C)
	(0,0,0) coordinate (G)
	(0,0,Sz) coordinate (S)
	foreach \v/\position in {A/below,B/below,C/below,S/above,G/below} 
	{(\v) node[dot,label=\position:{$\v$}]{}};
  \begin{scope}[A/.style={ball color=red!80},
 	 B/.style={ball color=orange!90},C/.style={ball color=blue!70},
	 S/.style={ball color=cyan!90}]
   \path[use as bounding box,tdplot_screen_coords] (-3,-1.5) rectangle (3,5.5);			
   \pgfmathsetmacro{\sdA}{screendepth(xi*Ax,xi*Ay,0)}
   \pgfmathsetmacro{\sdB}{screendepth(xi*Bx,xi*By,0)}
   \pgfmathsetmacro{\sdC}{screendepth(xi*Cx,xi*Cy,0)}
   \pgfmathsetmacro{\sdS}{screendepth(0,0,0)}
   \edef\lstsd{\sdA,\sdB,\sdC,\sdS}
   \foreach \X in {A,B,C,S}
   {%
   \expandafter\edef\expandafter\currsd\expandafter{\csname sd\X\endcsname}
   \setcounter{tdorder}{1}
   \foreach \sd in \lstsd
   {\pgfmathtruncatemacro{\itest}{ifthenelse(\sd<\currsd,1,0)}
   \ifnum\itest=1
   \stepcounter{tdorder}
   \fi}
   \begin{pgfonlayer}{layer\number\value{tdorder}}
	\def\tmpS{S}
	\ifx\X\tmpS
     \fill[S,tdplot_screen_coords] (S) circle[radius=2*R];
	\else
     \fill[style/.expanded=\X,tdplot_screen_coords] (\X) circle[radius=R];
	\fi
	%\typeout{\X\space on layer \number\value{tdorder}; \lstsd}
   \end{pgfonlayer}
   }
  \end{scope}
  \draw[help lines,dashed] (S) -- (A) (S)--(B) (S)--(C) (A)--(B) (A)--(C) (B)--(C) (A)--(G) (B)--(G) (C)--(G) (S)--(G);
 \end{tikzpicture}}
\end{document}
```

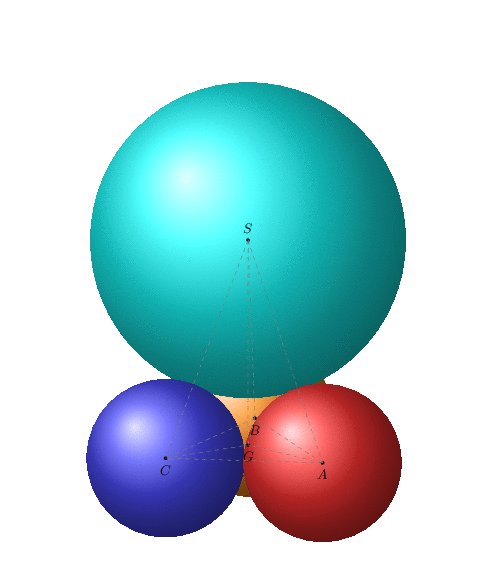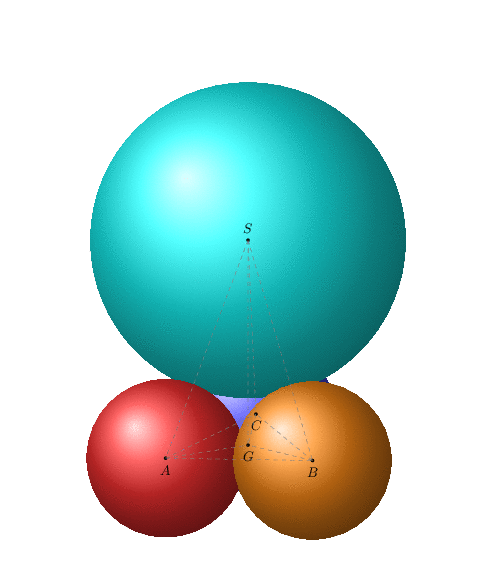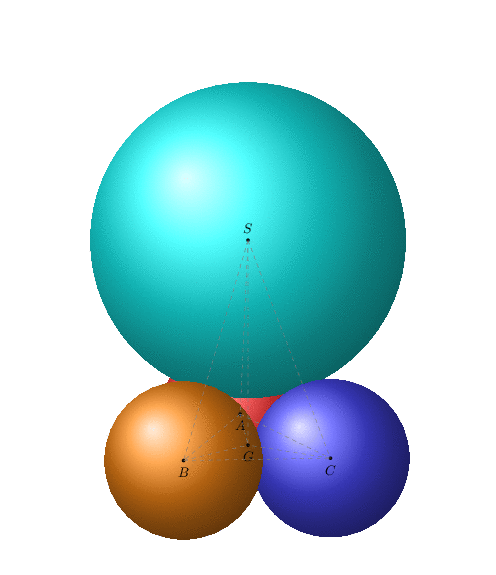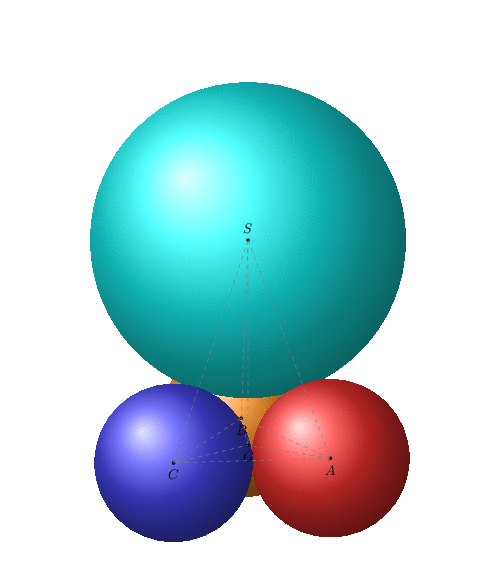
![ani.gif](/image?hash=e2700ee9557b25325bf73afe6605056e41daf04109b84a4433f81ad08177ca06)

Some of the routines here are part of the `3dtools` library, which got discontinued.

1 Answer